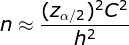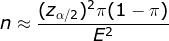如何确定抽样统计的最小样本量
作者:车东
在电视节目中经常看到关于选举的报道中经常会后有支持率的数字,例如:调查结果为
- a方支持率为45.3%;
- b方支持率为30.2%;
- c方支持率为8.5%;
- …
最后都会说明一下,此次电话调查的数量2352,置信度为95%﹐最大抽样误差为±2.5%。
抽样调查的典型情景:对一个大的集合(比如:数千万选民)做一次调查的成本较高,抽样调查可以低成本的用近似的(可接受的)数据反映实际情况;在用户调研中,也经常通过通过抽样调查的方式并对比打分的方法做评估。这里就需要了解置信度和抽样误差的概念。
1. 抽样误差
假如相同规模的抽样调查进行多次, 抽样均值在真实均值的上下波动,相对于整体均值的偏移波动就是抽样误差,而这个误差的分布是符合标准正态分布的,例如下图: 横轴为整体的均值,圆点是每次抽样的均值,而红色那次抽样就是加上误差后都未覆盖到均值线的情况);
2. 最小抽样量的计算公式
抽样量需要 > 30个才算足够多,可以用以下近似的误差/样本量估算公式;
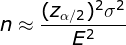
- n: 为样本量
 :方差,抽样个体值和整体均值之间的偏离程度,抽样数值分布越分散方差越大,需要的采样量越多
:方差,抽样个体值和整体均值之间的偏离程度,抽样数值分布越分散方差越大,需要的采样量越多- E: 为抽样误差(可以根据均值的百分比设定),由于是倒数平方关系,抽样误差减小为1/2,抽样量需要增加为4倍
 : 为可靠性系数,即置信度,置信度为95%时,
: 为可靠性系数,即置信度,置信度为95%时, =1.96,置信度为90%时,
=1.96,置信度为90%时, =1.645,置信度越高需要的样本量越多;95%置信度比90%置信度需要的采样量多40%
=1.645,置信度越高需要的样本量越多;95%置信度比90%置信度需要的采样量多40%
为了体现相对差距: 假设抽样均值为 y
相对抽样误差 h = E / y
变异系数 C= σ / y
3. 抽样误差估算表格
方差越大需要的样本量越多,数据离散度越低,需要的抽样量越少。
| 置信度 | 相对抽样误差(假设:C=0.4) | ||||
| 1% | 2% | 3% | 4% | 5% | |
| 95% | 6147 | 1537 | 683 | 384 | 246 |
| 90% | 4330 | 1082 | 481 | 271 | 173 |
如果是基于胜出率,支持率等: 分值为0/1状态分布,公式拟合为
π为按照经验得出的最后比例,在未知时π可取50%,待算出结果后再重新拟合,比例越悬殊需要的样本量越少。
| 置信度 | 相对抽样误差 | ||||
| 1% | 2% | 3% | 4% | 5% | |
| 95% | 9604 | 2401 | 1067 | 600 | 384 |
| 90% | 6765 | 1691 | 752 | 423 | 270 |
从而看出大部分的电话抽样调查:95%置信度的情况下,误差要控制在2%以内取样量一般在2000-5000。
转载来源:车东[Blog^2]